Active Matter
The material properties of living matter include a number of desirable qualities that have yet to be incorporated into inanimate materials. Examples are the self-healing ability of living materials and the ability to adapt to stress by self-strengthening mechanisms, as exhibited by tree limbs exposed to persistent wind or snow drifts. Another category is the ability for individual biological units to dynamically self-organize into larger ensembles as in the flocking behavior of birds, schooling of fish, and swarming of bacteria. At the sub-cellular level, active behavior is exhibited in cytoskeletal reorganization during replication and in the various forms of cellular motility, such as crawling (amoebae, macrophages) and flagellar driven propulsion (bacteria, protozoan). A related case, in which the flagellae propel fluid while the organism remains at rest also produces desirable material properties such as the self-cleansing mechanisms of ciliary fields on the lining of trachea.
Gabriel Popkin wrote a nice news feature for Nature on active matter called The physics of life. Brandeis is placed at the center of the research field!
The category of materials to which all these systems belong, as well as the field of inquiry devoted to their study is called Active Matter. Active matter consists of an assembly of objects, each of which consumes energy to generate continuous dynamics either propagating in space or oscillating in time.
Each microbot in Hiro Hamada's presentation in Big Hero 6 is an element that consumes energy and generates forces that propel it. Each microbot primarily interacts with nearest neighbors and each has the same set of instructions, analogously to an individual bird in a flock, or a fish in a school. Hiro's demonstration of self-organization of robot swarms isn't that far fetched!
Active matter is an active field. In the last decade, numerous exciting theoretical developments spanning approaches ranging from non-equilibrium statistical mechanics to hydrodynamics have produced a solid framework for which to base understanding and future inquiry of the disparate phenomena. The theories are based on the recognition that active matter exists far from equilibrium, that energy is consumed to generate stress and motion, and that the symmetry of the system dictates the nature of the collective behavior. Currently, experiments are lagging theory. This is because systems far from equilibrium choose many different paths to dissipate energy. So while the objective is to create materials in which the consumption of energy results in coordinated motion or self-strengthening, there are numerous other intervening chemical reactions that don't produce the desired action, but only generate heat and waste products.
See what we've achieved below.
Extensile Active Microtubule Bundles
Miles O'Brian made this video about our research on Active Matter for NSF's Science Nation.
The Fraden lab is involved in two collaborative projects in experimental Active Matter. Our goal is to develop robust systems that will serve as paradigms for investigations of active matter across different length scales ranging from the micro to macroscopic. The first is an in vitro biologic system based upon microtubules and kinesin motors that is intentionally simplified to contain the minimal number of biological components needed to exhibit active matter behavior. The second system is synthetic and is comprised of non-biologic materials that communicate, compute and actuate based on heterogeneous hydrogels containing the Belousov-Zhabotinsky oscillating chemical reaction.
Confined Active Matter
Extensile Microtubules, developed by the Dogic Lab, are a self-assembled by mixing microtubule (MT) filaments of a few microns length, motor clusters of several kinesins, and depleting polymer, which induces microtubule bundling of the filaments (Fig. 1c) that are of order 100 microns in length and a dozen filaments in cross section, while the kinesin clusters simultaneously bind to a pair of MT in a bundle. Microtubules are polar and kinesin motors are powered by ATP consumption to move directionally along the filament towards the “+” end. Kinesin clusters generate extensile interfilament sliding that drives the flow of the background fluid microtubules aligned with opposite polarity (Fig. 1d).

Fig. 1. Extensile microtubule system. (a) Four components. (b) Multivalent motor clusters.
(c) Microtubule (MT) bundles. (d) MTs with opposite polarity are driven to extend by motor clusters.
(e) Polar aligned MTs do not slide.
Unconfined active 2D nematics. The Dogic Lab discovered that when extensile microtubule bundles are sedimented onto a surfactant-stabilized oil-water interface they form dense quasi-2D active nematic liquid crystals. Uniformly aligned active nematics are inherently unstable. Unlike passive nematics, which don't flow in equilibrium, active nematics do flow spontaneously in the absence of external forces. However, unconfined active nematics generate turbulent-like flows that exhibit neither long-range order, nor net material transport.
Flow is driven by the spontaneous generation of defect pairs are created because active stresses amplify any bend fluctuation within an active nematic, which subsequently grows in amplitude. Above a critical deformation, the nematic director field self-fractures, generating a 1D fracture line that is terminated by a pair of oppositely charged disclination defects of charge +½ and -½. The +½ defects stream through the sample until being annihilated with an oppositely charged and stationary -½ defect. An activity dependent steady state is reached in which the rates of defect production and annihilation are matched.
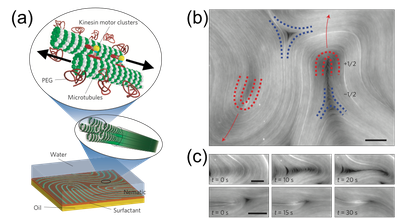
Figure. Unconfined 2D active nematic film. (a) Extensile microtubule bundles are confined to an oil/water interface. (b) Fluorescence microscope image of a MT active nematic with mobile +½ (red) and immobile –½ (blue) defects. (c) Image sequence illustrating the creation (top) and annihilation (bottom) of a ±½ defect pair. Scale bars, 50 μm. Video: Dogic Lab YouTube
Confined active 2D nematics. Dramatic new behavior arises when active nematics in 2D are confined; coherent long range flow. Confined active nematics are self-pumping fluids!
Our lab is using microfluidic manufacturing methods to construct ~100 micron sized annuli and disks and observe circulating flows in experiment. These geometries can be modeled theoretically and there are intriguing similarities and differences in the behavior that are subjects of active (pun intended) investigation in our lab.
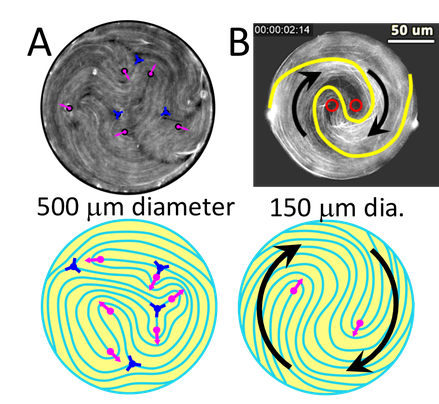
Figure. 2D nematics confined to disks of different radii. (A) For large diameters, the nematic behaves similarly to unconfined 2D nematics (Fig. 2), exhibiting turbulent flow with pairs of +1/2 and -1/2 defects created and destroyed at a steady state. (B) As confinement is increased, the director adopts a Yin Yang pattern characterized by a pair of co-rotating +½ defects which undergo spontaneous and continuous flow. See videos below.
Video. (Top) Fluorescence microscopy. (Bottom) Simulation. Director field on the left. Color indicates order parameter, which is low in the vicinity of the defect cores. Velocity field on the right. Vorticity in color.
Videos: Achini Opathalage & Mike Norton. FradenLab YouTube.
Confined Active Gels. Unconfined 3D active gels generate turbulent flow with no net transport. We discovered that 3D confinements and boundaries robustly transform turbulent-like dynamics of bulk active fluids into self-organized coherent macroscopic flows that persist on length scales ranging from micrometers to meters and time scales of hours. The transition from turbulent to a coherently circulating state is not determined by an inherent length scale of the active fluid, but is rather controlled by a universal criterion that is related to the aspect ratio of the confining channel. Coherent flows robustly form in channels with square-like profiles and disappear as the confining channels become too thin and wide or too tall and narrow. Consequently, this transition to coherent flows is an intrinsically 3D phenomenon that is impossible in systems with reduced dimensionality. Analysis of the microtubule network structure reveals that the transition to coherent flows is accompanied by the increase in the thickness of the nematic layer that wets the confining surfaces. The spatial variation of the nematic layer can be correlated to the velocity profiles of the self-organized flows.

Figure: Turbulent flows (right) occur in high aspect ratio channels. Decreasing the aspect ratio of the annulus induces a transition from turbulent to globally coherent flows of a confined active isotropic fluid (left). The left and right half-plane of each annulus illustrate the instantaneous and time-averaged flow and vorticity map of the self-organized flows. The transition to coherent flows is an intrinsically 3D phenomenon that is controlled by the aspect ratio of the channel cross section and vanishes for channels that are either too shallow or too thin.
Video: Flow in confined toroids and cylinders as a function of aspect ratio. Coherent flow occurs when the aspect ratio of the largest to smallest dimension is less than 3:1. Velocity and vorticity in left panels, fluorescence microscopy of tracer beads in right panels. Video: Kun-ta Wu, FradenLab YouTube
Video: Motion of toroidally confined active microtubules (red) and tracer particles (green). Height and width of the toroid are 80 and 200 microns, respectively. The movie was taken with a confocal microscope, and microtubules and bead tracers are indicated in red and green, respectively. Flow rates of microtubules and tracers reveal no measurable differences. Time stamp is hour: minute: second. Video: Kun-ta Wu, FradenLab YouTube

In mirror-symmetric geometries, the coherent flows can have either handedness. Ratchet-like chiral geometries establish geometrical control over the flow direction.
Video. Coherent flows in 12- and 1-tooth CCW and CW ratchets. Decorating the toroid outer surface with notches induced coherent flows in the direction of same handedness. Even one notch is sufficient to control flow direction. The notch sizes are ~300 microns. Top two ratchets (left, CCW; right, CW) have 12 teeth, and bottom ones (left, CCW; right, CW) have only 1 tooth. Heights are 1.3 mm. Time stamp is hour: minute: second. Video: Kun-ta Wu, FradenLab YouTube
Video. Coherent (left) and incoherent (right) motion of active microtubule networks confined in toroids. In a high aspect ratio toroid (right, height = 100 microns, width = 500 microns), microtubules generate a turbulent flow. In a low aspect ratio toroid (left, height = 400 microns, width = 500 microns), microtubules generate a self-organized coherent flow. Time stamp is hour: minute: second.
Video: Kun-ta Wu, FradenLab YouTube
PNAS e2115895119 (2022). DOI: 10.1073/pnas.2115895119
Multiscale Microtubule Dynamics in Active Nematics
Physical Review Letters 127, 148001 (2021). DOI: 10.1103/PhysRevLett.127.148001
Submersed micropatterned structures control active nematic flow, topology, and
concentration
PNAS 118, e2106038118 (2021). DOI: 10.1073/pnas.2106038118
Machine learning forecasting of active nematics
Soft Matter 17, 738-747 (2021). DOI: 10.1039/d0sm01316a
Optimal Control of Active Nematics.
Physical Review Letters 125, 178005 (2020). DOI: 10.1103/PhysRevLett.125.178005
Dynamics of an
active nematic under topologically incommensurate confinement
PHYSICAL REVIEW E 97, 012702 (2018)
Supplementary movies