Non-linear chemical dynamics

Synthetic active tissue

Living matter possesses remarkable material properties, such as the ability to sense the environment, make decisions based on sensory input, and through self-propulsion, move in the direction of choice. The simplest single cellular organism, the bacterium, possesses these properties, as do many multi-cellular organisms. Some bacteria and amoeba, such as Dictyostelium exhibit chemotaxis – or navigate along chemical gradients to forage for food. In other circumstances, such as starvation, individual Dictyostelium communicate with each other through a chemical reaction-diffusion mechanism and self-organize into a kind of tissue where the single cells aggregate into a fruiting body for survival. Some bacteria aggregate and then protect themselves by enveloping themselves in a starch coat called a bio-film. These materials have the ability to heal themselves. The goal of this project is to create a new class of materials, which have properties heretofore only associated with living matter. Like living matter, these materials will be active in the sense that they must consume energy in order to function, but will be entirely synthetic with no biological components at all. Combining methods of experiment, simulation and theory and personnel spanning the disciplines of neuroscience, computer science, physics and chemistry we will lay the scientific framework to create materials that have properties like trees that grow thicker and stronger in response to stress imposed by wind or snow, or muscle tissue, which increases strength in response to need (or exercise).

The materials we will study are based on the Belousov-Zhabotinsky (BZ) chemical reaction. The BZ system produces an oscillating redox reaction of a metal ion. In thermodynamically closed systems the BZ oscillations can occur 100 times, but will last forever in an open system in which the BZ reactants are continuously fed into the solution. In analogy with living matter, we produce “cells” by isolating the aqueous BZ reagents in either gels or in emulsion droplets where oil forms the continuous phase. We combine individual cells to create a “tissue” composed of many cells separated by a matrix or fluid. Cells communicate through the diffusion of BZ chemicals through the intervening medium and can initiate "morphogenesis" in which BZ droplets first chemically differentiate through a Turing instability and then physically differentiate through osmotic stress, or form "neural networks" capable of generating spatiotemporal patterns corresponding to those controlling gaits in animal locomotion. 

Quadrupeds have particular gaits that are controlled by a single neural network called a Central Pattern Generator. How does a single network generate the spatiotemporal firing of neurons to activate the legs to move in a particular gait?

Our paper, Pattern formation in a four-ring reaction-diffusion network with heterogeneity, is the result of over a decade of hard work in both theory and experiment, which raises a series of questions. What did we set out to do and why? Why did it take so long and why did we stick at it through all the difficulties? At the end, what did we accomplish and who cares?

We started out studying symmetric networks in which the nodes are reactors containing identical oscillating chemical reactions and the links between nodes are identical and confined to nearest neighbor. We picked such networks because they are the simplest network of chemical reactions that produce interesting and functional behavior. We focus on neural networks known as “central pattern generators” (CPG) responsible for coordinating autonomous animal locomotion. What problems to CPGs solve? When you walk, you don’t think about the sequence of lifting your knee, swinging your leg, striking your heel, and pushing off on your toes. This is done unconsciously. Likewise, when you decide to switch from a walk to a run, your gait changes, but you don’t think about the new rhythms demanded for running. Once you’ve made the conscious decision to change gaits, you don’t have to think about how to maintain the new gait; running and walking are automatic, hardwired behaviors. How do we living organisms accomplish this? One possible solution is to have a different set of autonomous neural networks responsible for each gait. But this isn’t the solution adopted by living organisms. Instead, we use one neural network that is capable of supporting multiple gaits. Furthermore, the neurons in the CPG are highly similar to one another and are wired together in a highly symmetric fashion, which is economical from both a design and manufacture perspective.

How do we animals manage to have one neural network that robustly exhibits a multiplicity of stable behaviors? The theory of dynamical systems provides a hypothesis. It turns out that a system of self-driven oscillators connected together in a symmetric network must exhibit a rich variety of spatio-temporal patterns, independent of the nature of the individual oscillators and wholly dependent on the symmetry of the network.

The design of networks that generate desired spatiotemporal patterns is a great challenge because universal organizing principles for far-from-equilibrium systems are exceedingly rare. Exploiting network symmetry is one way to meet this challenge. Symmetries place hard constraints on the network dynamics of self-driven oscillators by dictating that certain transient features and steady-state patterns must exist. However, the robustness of this class of theories to symmetry-disrupting imperfections is untested in free-running (i.e., non-computer-controlled) systems. Here, we develop a model experimental reaction-diffusion network of chemical oscillators to test applications of the theory of dynamical systems with symmetries in the context of self-organizing systems relevant to biology and soft robotics. The network is a ring of four microreactors containing the oscillatory Belousov-Zhabotinsky reaction coupled to nearest neighbors via diffusion. Assuming homogeneity across the oscillators, theory predicts four categories of stable spatiotemporal phase-locked periodic states and four categories of invariant manifolds that guide and structure transitions between phase-locked states. In our experiments, we observed that three of the four phase-locked states were displaced from their idealized positions and, in the ensemble of measurements, appeared as clusters of different shapes and sizes, and that one of the predicted states was absent. We also observed the predicted symmetry-derived synchronous-clustered transients that occur when the dynamical trajectories coincide with invariant manifolds. Quantitative agreement between experiment and numerical simulations is found by accounting for the small amount of experimentally determined heterogeneity in intrinsic frequency. We further elucidate how different patterns of heterogeneity impact each attractor differently through a bifurcation analysis. We show that examining bifurcations along invariant manifolds provides a general framework for developing intuition about how chemical-specific dynamics interact with topology in the presence of heterogeneity that can be applied to other oscillators in other topologies.

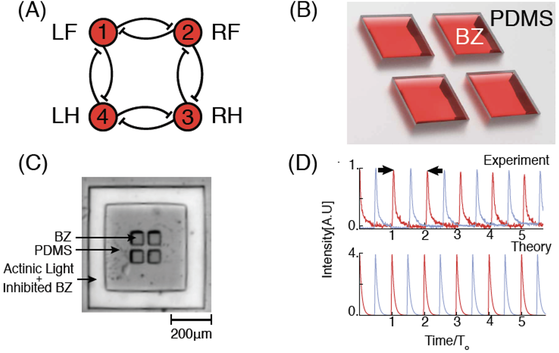
(a) Schematic of a network of a ring of four inhibitory coupled oscillators. Indexing of nodes is indicated as either a number (1,2,3,4), or a leg of a quadruped (LF, RF, RH, LH) with L left, R right, F front, and H hind. (b) Schematic of the experimental system. The reactors are divots in the PDMS, filled with BZ and sealed between two glass plates. (c) Photograph of BZ-filled four-ring network. Light illuminates BZ in a channel surrounding the network, activating the photosensitive catalyst to provide a constant chemical boundary condition. (d) Two adjacent reactors (red and blue traces) in the network oscillating 180 degrees out of phase with each other. Top: Measured transmitted intensity versus time. Bottom: Simulated oxidized catalyst concentration (mM) versus time. In both, To is the period at steady state of ∼300 s in experiment and ∼250 s in theory and is indicated by the two arrows.

We want to investigate open systems, in which fuel is fed in and waste products removed, because open reactors can be maintained in steady out-of-equilibrium states forever. Our BZ oscillator networks are closed systems. Each oscillator contains 1 nl and once all the fuel is consumed, the oscillations cease. Our BZ oscillators execute several hundred cycles between birth and death, but not all the oscillations can be used for studies of network dynamics. A certain amount of time in the beginning is needed for the frequencies and phase of the network to lock. Here it takes about 4 oscillations for the oscillators to frequency stabilize and about 30 - 40 oscillations for the network to phase lock. The system stays phase locked for another 30 - 40 oscillations, but then, although the individual oscillators will continue to oscillate for another 100 or more cycles, the oscillators become noisy.  So practically, our BZ networks approximate open systems for about 80 oscillations. This limits the duration of transient dynamics that can be studied in networks.  

Left table: Symmetry required invariant manifolds for an oscillator network possessing square symmetry. The first four classes of manifolds are phase-locked states.  The column marked “Phase” graphically indicates the spatiotemporal pattern with symbols representing the phase in percentage of a full cycle: white circle, 0%; white/black, 25%; black circle, 50%; black/white, 75%. The second four classes of manifolds are symmetrically clustered states, related by arbitrary phase shifts. The graphical representation of nodes in the column “Phase” have solid, striped, or dot motifs. Different motifs are related by an arbitrary phase shift. Similar motifs with opposite background colors are antiphase with each other.

Right Plot: Point invariant manifolds have all the phase differences fixed. In the phase space of phase differences, they are points. Linear invariant manifolds have one phase that is not fixed and are lines in the phase space of phase differences. Planar invariant manifolds have two phase differences that are not fixed and are planes in the phase space of phase differences.

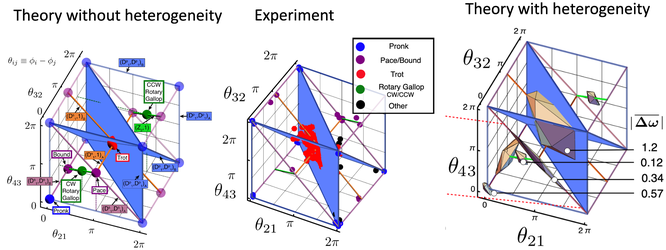
We studied the phase dynamics of 352 independent 4-ring oscillators. We found that 186 of them locked into a steady state in which the phase differences between the 4 oscillators did not change. The plot on the left represents the phase space of oscillator phase differences for identical oscillators. The plot in the center represents the experiment in which we observed the predicted Pronk, Pace/Bound and Trot states, but not the predicted Rotary Gallop state. The plot on the right extends the theory to account for the experimentally observed amount of heterogeneity. We find agreement between theory and experiment with this extension of the theory.

Understanding how network structure controls spatiotemporal pattern formation remains a central problem in network science. When we extend the theory of homogeneous, symmetric networks to account for the experimentally determined heterogeneity of the oscillator frequency, we find agreement between theory and experiment.  We demonstrate that with proper accounting of heterogeneity, symmetry can be used to rationally engineer spontaneously organizing reaction-diffusion networks, an important category that includes biological systems such as neural networks. In particular, we studied a ring of four BZ chemical oscillators, which symmetry-based theories predict are capable of generating the spatiotemporal patterns known as the gaits of a quadruped. In this work, we experimentally validate that symmetry dictates function in weakly coupled reaction-diffusion systems even in the presence of heterogeneity.

Meghna Chakrabarti of RadioBoston on WBUR (Boston's NPR news station) interviewed Seth and Irv about the lab's experimental confirmation of Alan Turing's theory of morphogenesis. 

Link to RadioBoston interview webpage.

A statue of Alan Turing at the Bletchley Park Museum, poring over an Enigma machine. (Duane Wessels/Flickr)

Animated histogram displayed with a nonlinear timescale (time bar in right panel). Drops demonstrating morphogenesis plotted as fraction of original drop area vs. fraction of original drop intensity. The color coded line tracks the center of each peak as a function of time. Drops are initially homogenous in both intensity and size. Bright drops are oxidized, dark drops reduced. At intermediate times the drops undergo a Turing case (d) instability; heterogeneous in intensity, or oxidation state, but homogenous in size. This is equivalent to chemical, but not physical differentiation. At later times drops are heterogeneous in both oxidation state and size, i.e. chemical differentiation precedes morphogenesis. The oxidized (bright) drops shrink and reduced (dark) drops swell. Chemical conditions: 200mM MA, 0.4mM Rubipy, 0mM NaBr, 80mM H2SO4, 300mM NaBrO3, 3mM Ferroin, 0.05 x 1mm capillary, initial drop size ∼ 66μm.

Testing Turing's Theory of Morphogenesis in Chemical Cells

Nathan Tompkins, Ning Li, Camille Girabawe, Michael Heymann, G. Bard Ermentrout, Irving R. Epstein, and Seth Fraden, Proceedings of the National Academy of Sciences 111, 4397–4402 (2014).
DOI: 10.1073/pnas.1322005111.

The BZ chemistry is complex, but can be understood semi-quantitatively at a detailed level involving a few dozen chemical species. Focusing on the rate limiting reactions allows a simplified description in terms of two species; an activator and an inhibitor, which interact in three distinct steps. First, the metal ion is in the reduced state. The inhibitor suppresses oxidation of the metal ion while a slow process consumes the inhibitor. Second, once the inhibitor falls below a critical threshold, the activator is unleashed and an autocatylic reaction leads to a rapid oxidation transition consuming all the reduced metal ion. Third, once the oxidation is complete a slow process reduces the oxidized metal ion while simultaneously producing the inhibitor, thus restarting the oscillation. 

A limited subset of the aqueous BZ chemicals permeates through the hydrophobic intercellular medium giving rise to intercellular communication. In the video above, the 7 drops in a ring are inhibitory coupled. Each drop acts to inhibit its immediate neighbor. But frustration arises because there are an odd number of drops in the ring leading to the generation of a beautiful heptagram. Videos: Nate Tompkins. FradenLab YouTube.   

Inhibitory coupled BZ drops adopt a spatiotemporal pattern such that neighbors oscillate with the largest possible phase difference. (Left) Real space. Video of oscillations in a ring of 7 BZ drops. Colors label each drop. Flashes occur when a drop oxidizes. (Right) Phase difference space. Location of colored disks on circle represents phase difference between drops at the moment of the oscillation. The white disk rotates at the average oscillation frequency. The white disk crosses a colored disk when the corresponding colored drop oxidizes in the left video frame.  The maximal phase difference between neighboring drops is 3π/7 and 4π/7; e.g. in the left video frame the red drop has a mauve and orange drop as nearest neighbors, but in the right video frame the mauve and orange colored disks appear as opposite as possible from the red disk at positions representing phase differences of 3π/7 and 4π/7, as Turing theoretically predicted. Videos: Nate Tompkins. FradenLab YouTube.   

We also introduce light sensitive catalysts that allow external control of the reaction. We fabricate cells between 10 microns and 200 microns in diameter. Using a computer programmable illumination system we can individually “address” each cell and control the phase of the chemical oscillator using light. When confined to a two dimensional layer we can simultaneously image and control about 1000 cells.

Pattern formation in a four-ring reaction-diffusion network with heterogeneity
Phys. Rev. E 105, 024310 (2022). DOI: 10.1103/PhysRevE.105.024310 
Supplement with tons of movies on YouTube.

Partition, Reaction, and Diffusion Coefficients of Bromine in Elastomeric Polydimethylsiloxane
J. Phys. Chem. B (2021). DOI: 10.1021/acs.jpcb.1c01552

Impact of PDMS-Based Microfluidics on Belousov−Zhabotinsky Chemical Oscillators
Journal of Physical Chemistry B 124, 11690-11698 (2020). Supplement. DOI: 10.1021/acs.jpcb.0c08422

Dynamics of Reaction-Diffusion Oscillators in Star and

            other Networks with Cyclic Symmetries Exhibiting Multiple Clusters
Phys. Rev. Lett. 123, 148301 (2019).  DOI: 10.1103/PhysRevLett.123.148301

Engineering reaction–diffusion networks with properties of neural tissue
Lab on a Chip 18, 714 - 722, (2018); DOI: 10.1039/c7lc01187c 

Configurable NOR gate arrays from Belousov-Zhabotinsky micro-droplets

Eur. Phys. J. Special Topics 225 (1),211-227 (2016); DOI: 10.1140/epjst/e2016-02622-y 

Creation and perturbation of planar networks of chemical oscillators

Chaos 25, 064611 (2015); DOI: 10.1063/1.4922056.

Tunable diffusive lateral inhibition in chemical cells

Eur. Phys. J. E 38, 18 (2015); DOI 10.1140/epje/i2015-15018-3.

Giant Volume Change of Active Gels under Continuous Flow
JACS (2014); 
Supplement; movie S1, oscillating gel annulus; movie S2, oscillating gel array

DOI: dx.doi.org/10.1021/ja503665t 

Combined excitatory and inhibitory coupling in a 1D array of Belousov- Zhabotinsky droplets

Phys. Chem. Chem. Phys. 16, 10965-10978 (2014); DOI:10.1039/C4CP00957F. 

Testing Turing's Theory of Morphogenesis in Chemical Cells

PNAS 111, 4397–4402 (2014); DOI: 10.1073/pnas.1322005111. 

Coupled oscillations in a 1D emulsion of Belousov–Zhabotinsky droplets

Soft Matter 7, 3155 (2011), DOI: 10.1039/c0sm01240h.