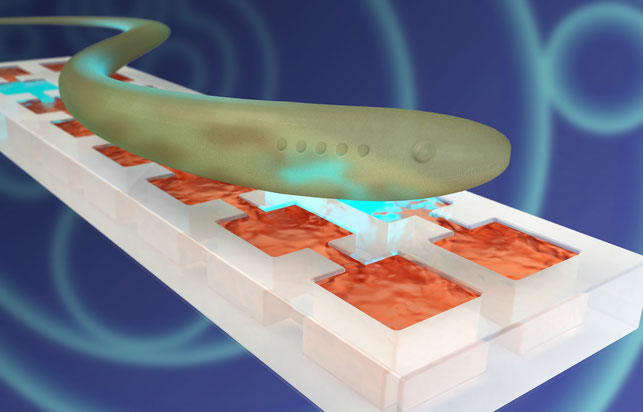
Soft Robots
We aspire to build soft robots that execute the rhythmic undulations of a swimming Blue Ribbion Eel. Central pattern generators are a class of neural networks found in the autonomic nervous system that perform cyclic functions and govern motions such as walking, the beating of the heart and the peristaltic motion of the digestive system. The networks produce rhythmic pulses distributed in space that coordinate muscle contractions. Minimal models treat individual neurons as self-driven non-linear oscillators that when coupled together produce complex spatio-temporal patterns. Turing recognized that chemical reactions were capable of producing self-driven oscillators and elucidated the conditions in which diffusively coupled chemical networks exhibit spontaneous spatio-temporal pattern formation. Guided by this insight, we exploit the self-organizing properties of reaction-diffusion systems to engineer a synthetic substrate that emulates the autonomous spatio-temporal patterns exhibited by central-pattern generators by designing and fabricating networks of coupled BZ chemical oscillators that generates the spatio-temporal pattern produced by a swimming eel.

Figure. Example of a biological central pattern generator. (A) Lampreys swim by generating waves of transverse displacement down their spinal column. Red areas indicate regions of muscle contraction left of the spinal cord, blue indicates regions of muscle contraction right of the spinal cord. (B) Schematic diagram of an exposed lamprey spinal cord with ventral roots. Each vertebra has a pair of neurons, situated to the left and right of the column. (C) Schematic time trace of electrical activity for each of the corresponding pairs of ventral roots shown in (B). In red (blue) traces show the voltage of neurons on the left (right) side of the spinal cord. Neurons on opposite sides of a vertebra fire with a relative phase shift of 180°, while neurons on the same side fire with a small phase lag between neighboring vertebrae, producing the displacement wave shown in (A). (D) Schematic of lamprey central pattern generator realized as a reaction–diffusion network. Each circle represents an oscillating chemical reaction. Links with nails (arrows) indicate inhibitory (excitatory) coupling.
Experiment (left) and theory (right) of a biometic implementation of the Central Pattern Generator of an eel.
Videos: Thomas Litschel & Mike Norton. FradenLab YouTube.
Neural tissue evolved 3.5 billion years after the origin of life, which is a testament to its complexity, and is found in almost all multicellular life, which is a testament to its importance. At the coarsest level of description, neurons are non-linear oscillators that when coupled together in tissue through excitatory and inhibitory connections give rise to complex spatio-temporal patterns. Extrapolating from this general definition of a neuronal network, we posit these dynamics can be captured on an abiologic reaction-diffusion platform. We use soft lithography methods that allow the engineering of synthetic reaction-diffusion networks. We employ the well-known oscillatory Belousov-Zhabotinsky reaction and develop methods to create diffusively coupled networks over which we design (i) the topology of the network, the (ii) boundary and (iii) initial conditions, (iv) the volume of each reactor, (v) the coupling strength, and (vi) whether the coupling is of an inhibitory or excitatory nature.
An application for the reaction-diffusion based networks developed here is to the field of soft robotics, where the central pattern generator will serve as the controller of an artificial musculature comprised of chemomechanical gels coupled to the BZ layer.
This paper was highlighted by one of our sponsors, the US Army.